​科学家是怎么证明多维空间的存在（125个科学难题解秘之第四讲）

科学家是怎么证明多维空间的存在（125个科学难题解秘之第四讲）

《科学》杂志曾于创刊125周年之际发布过125个推动基础科学研究的科学难题，王江火在此后的文章中将通过统一信息论来逐一尝试解决这些难题。本文将开始第四讲，揭示《科学》杂志所公布的“全世界最前沿的125个科学问题”之第五部分（天文学）之第一个问题——“空间中有多少个维度？”。

有关这个问题，已经被现代科学上的幻想家搞得很混乱了，他们仅凭想当然就认为宇宙应该存在高于三维空间的许多多维空间。在平行宇宙理论中，认为此平行宇宙本身至少有一个5维空间。在弦理论中，认为各种基本粒子都是由很小很小的线状弦组成的，在众多现象难以用理论解释的情况下，爱德华·维顿提出了11维空间的概念。

实际上，多维空间都是基于数学概念想象的，现实中只有0维和三维空间，客观上也没有绝对的一维和二维空间，这两种所谓的空间只能是依赖三维空间而设想的空间概念。除此之外，至今没有发现其他维度的空间，或者是即使存在也无法为人类所感知，探讨这个问题已经属于属于形而上学而没有现实意义。即便按照数学推论，宇宙间除了0维、三维外，最多只可能存在四维和五维空间，但这也仅仅是理论上的可能性，最可能最现实的还是0维、三维空间。下面将通过统一信息论来解决这个问题。

根据统一信息论，宇宙大爆炸后，由于能量子的相互掣肘，光子将会使其震荡或自旋的速度降低到光速以下，并同时转化成具有同样信息量和能量的质点，同时被集合成极限粒子，并将质点所含有的能量分布到整个结构形成质量。这个过程同时也需要伴随着时空的产生，而时空的三维却需要信息才能彰显，这个过程不仅是客观的，同时也涉及到信息认知的认识问题，其复杂性可想而知。但无论怎样，有一个基本问题是可以明确的：信息点要被集合成物质，除了要将信息质点化并形成时空之外，还需要在三维空间的每个维度上至少有两个质点，也就是说，三维空间的每个维度上至少具备两个质点是物质存在的最基本条件。因此，组成物质的最小质点量是2×2×2=8个质点。再考虑到标准直线只能由两个质点复合而成的情况，由8个质点组成的基本粒子将因此而具备最稳定状态。如此，由8个质点组成的正方形物质就成为了物质的最小单位，即极限粒子。

上述是极限粒子形成三维空间的一种情况，那么，还会不会存在形成多维空间的情况呢？从理论上讲这是可能的，因为能量子既然能够结合成三维向度的三维空间，那么也应该能够结合成三维以上的多向维度空间，这首先需要我们搞清楚“维”的概念。“维”是指空间的向量，比如0维是指单纯的一个点；1维只有一个向量的长度；2维是有两个向量的空间平面世界；3维则是有3个长宽高（或上下、前后、左右）等三个向量的立体世界。因此，有几个向量就有几维的空间，

极限粒子要想形成多维度空间的最小单元体，需要具备两个条件：其一，极限粒子的所有向度的单元长度为宇宙最短的普朗克尺度，这样才能体现极限粒子的极限性；其二，极限粒子为正多面体，这是由于极限粒子所有向度的单元长度为宇宙最短的普朗克尺度造成的，同时也是出于各维度完全同质性的要求。据这样两个条件，我们只需要根据极限粒子所可能形成的正多面体的每个顶点能够具备几个向度，就可以判断所形成空间的维度了。

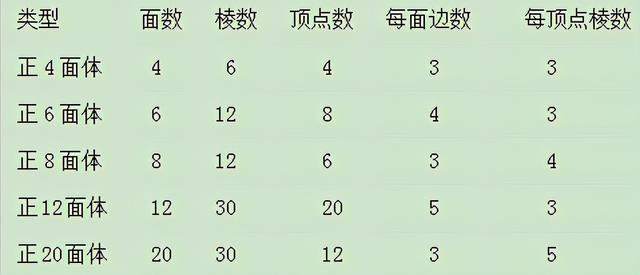
所谓正多面体，是指多面体的各个面都是全等的正多边形，并且各个多面角都是正多面体全等的多面角。例如，正四面体（即正棱锥体）的四个面都是全等的三角形，每个顶点有一个三面角，共有四个三面角，可以完全重合，也就是说它们是全等的。正多面体的种数很少。多面体可以有无数，但根据推论，正多面体只有正四面体、正六面体（正方体）、正八面体、正十二面体、正二十面体五种（见上图），这样，我们就可以根据这些正多面体所形成的每个顶点的棱数，就可以判断极限粒子所可能形成的向量，从而就可以判断宇宙可能形成的维度空间的种类。

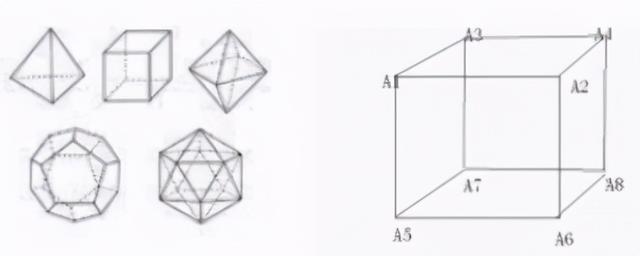
从上表不难发现，正多面体顶点的棱数只有3棱、4棱、5棱等三种，也就是说极限粒子只可能形成3维、4维、5维空间。其中三维空间的情况有三种：极限粒子为正4面体、正6面体、正12面体，但就空间结构的稳定性和维度的适用性而言，3维空间的极限粒子应该以正6面体的正方体最为妥当；4维空间的极限粒子为正8面体，在这儿所说的4维空间不同于爱因斯坦在他的《广义相对论》中提及的“四维时空”概念，爱因斯坦“四维时空”是在不过是在三维空间的架构上又多加了一条时间轴，而这条时间的轴是一条虚数值的轴，其实还是3维度空间；而5维空间的极限粒子则只有正20面体一种情况。

由此可以判断，宇宙只可能存在3维、4维、5维空间，而由于形成它们的极限粒子的形态不一样，宇宙也不存在不是由极限粒子构成的绝对空间，所以上述三种维度的空间是不能相互混溶在一起的，如果这三种空间真实存在，那么也只能分处于宇宙不同的区域，或许它们之间有一个明显的分界线，但无论怎样，如果4维、5维空间存在的话，它们也不是超自然存在，它们终会为人类所认知；而如果4维、5维不能被发现的话，那么它本就不会属于客观存在。另外，0维是电磁波、光、能量的存在方式，但无法用空间概念来表述，因此，零维虽然是客观存在，但不属于空间范畴。而1维和2维只是几何逻辑的概念，现实中并不存在。

所以，宇宙最有可能的就是三维空间，其他多维空间是几乎不可能存在的，超过3维的多维空间很可能只是形而上学的猜测而已。大咖们就不要瞎猜乱想了，人的生命是有限的，请多把精力用在现实中吧！

,