​113是质数吗（113是不是质数）

113是质数吗（113是不是质数）

撰文 | Patrick Honner

翻译 | C&C

审校 | 藏痴

如果你一直关注这个月的数学新闻，你就会知道35岁的数论家詹姆斯·梅纳德

（James Maynard）

获得了

菲尔兹奖

——数学家的最高荣誉。据新闻报道，梅纳德喜欢的数学问题“简单到足以向高中生解释，但却足以难倒数学家几个世纪”，其中一个简单的问题是：当你沿着数轴移动时，总会有靠在一起的质数吗？

你可能已经注意到数学家对

质数

很着迷。是什么吸引了他们？也许是因为质数体现了数学中一些最基本的结构和奥秘。质数描绘了乘法的世界，它允许我们用唯一的因式分解来分类每一个数字。但是，即使人类从乘法诞生之初就开始研究质数，我们仍然不确定质数会出现在哪里，它们的分布范围有多广，或者它们的距离有多近。就我们所知，质数的分布没有简单的规律。

我们对这些基本概念的迷恋导致了数百种

不同类型

质数的发明或发现：梅森质数

(2

^

?-1形式的质数)

，平衡质数

(两个相邻质数的平均值)

，索菲·日尔曼质数

（p是质数同时2p + 1也是质数）

，如此等等。

人们对这些特殊质数的兴趣源于对数字的研究和新发现的获得。“

数位敏感质数

(digitally delicate primes)

”也是如此。最近，数位敏感质数产生了一些关于最基本问题的惊人结果：

某些类型质数的出现频率到底有多少

？

注意q不可能在上面的质数列表中，因为它比列表中所有的数都大。所以如果存在一个有限的质数列表，那么q就不是质数。但如果q不是质数，那么它一定能被除它和1以外的数整除。反过来，这意味着q

一定能

被列表中的某个质数整除，但由于q的构造方式，q除以链表上的任何数，余数都是1。显然q既不是质数也不能被任何质数整除，出现这样矛盾的原因是假设质数数量有限。因此，为了避免这个矛盾，实际上必须有无穷多个质数。

考虑到质数有无穷多个，你可能会认为所有种类的质数都很容易找到，但数学家接下来要学习的一件事是质数可以有多分散。一个被称为

质数间隙

的关于相邻质数之间间隔的简单结果，说明了一些令人惊讶的事情。

前10个质数——2、3、5、7、11、13、17、19、23和29——之中，你可以看到由一个或多个

合数

(不是质数的数，如4、12或27)

组成的空隙。你可以通过计算其中合数的数目来测量这些间隙：例如，在2和3之间有一个尺寸为0的间隙，在3和5、5和7之间有一个尺寸为1的间隙，在7和11之间有一个尺寸为3的间隙，等等。这个列表中最大的间隙是23和29之间的5个合数——24、25、26、27和28。

现在让我们看看一个令人难以置信的结果：

质数间隙可以是任意长的

。这意味着存在相邻的质数，它们之间的距离是无穷远。也许同样令人难以置信的是，这个事实非常容易被证明。

我们上面已经有了一个长度为5的质数间隙。会有长度为6的吗？我们不必寻找质数表来找到这样的例子，我们可以自己构造一个。为此，我们将使用基本算术公式中使用的

阶乘函数

：根据定义，整数n的阶乘n!=n×(n?1)×(n?2)×…×3×2×1，例如3!= 3×2×1=6和5!=5×4×3×2×1=120。

现在让我们来构造我们想要的质数间隙。考虑以下连续的数字序列：

7!+2， 7!+3， 7!+4， 7!+5， 7!+6， 7!+7

因为7!=7×6×5×4×3×2×1，我们序列中的第一个数字，7!+2可以被2整除，你可以通过分解看出:

7!+2=7×6×5×4×3×2×1+2=2(7×6×5×4×3×1+1).

同样，第二个数字，7!+3，能被3整除，因为 :

7!+3=7×6×5×4×3×2×1+3=3(7×6×5×4×2×1+1).

同样，7!+ 4能被4整除，7!+ 5能被5整除，7 !+ 6能被6整除，还有7!+ 7 能被7整除，因此7! + 2， 7! + 3， 7! + 4， 7! + 5， 7! + 6， 7! + 7是六个连续的合数。我们的质数间隙至少是6。这种策略很容易概括。序列 n!+2， n!+3， n!+4， …， n!+n是一个由n?1个连续合数组成的序列，这意味着，

对于任何n，存在一个长度至少为n?1的质数间隙

。

这表明存在着任意长的质数间隙，所以在自然数列表中，有一些地方离最近的质数相差了100个，1000个，甚至10亿个数字。

从这些结果中可以看出一种典型的矛盾。质数有无穷多个，而连续的质数也可以相距无穷远。更重要的是，有无限多个相邻的质数。大约10年前，张益唐的开创性工作引发了一场缩小间隙和证明

孪生质数猜想

的竞赛。孪生质数猜想断言，有无穷多对相差仅为2的质数。孪生质数猜想是数学中最著名的开放问题之一，詹姆斯·梅纳德

（James Maynard）

为证明这一难以捉摸的结果做出了自己的重大贡献。

这种矛盾也出现在最近关于所谓的

数位敏感质数

的研究结果中。为了了解这些数字是什么，以及它们可能出现的位置，请花点时间思考下面这个奇怪的问题：有没有一种两位数的质数，只要其中一位数有所变化，就一定会成为合数？

为了了解数位敏感，我们来试试数字23。我们知道它是个质数，但如果你

改变

它的个位数会怎样？20、22、24、26、28都是偶数，因此是合数；21能被3整除，25能被5整除，27能被9整除。到目前为止，一切顺利。但如果把个位换成9，得到29，仍然是质数。所以23

不是

我们要找的质数。

37呢？正如我们上面看到的，我们不需要检查偶数或以5结尾的数，所以我们只检查31、33和39。31也是质数，所以37也不行。

这样的数字存在吗？答案是

肯定

的，但我们必须一直算到

97

才能找到它：97是质数，但91 (能被7整除)、93 (能被3整除) 和99 (也能被3整除) 都是合数，除此之外就是偶数和95。

如果你把质数的任何一个数字换成其他数字，它就不再是质数，那么这个质数就是“

敏感的

”。到目前为止，我们看到97在个位数字上很敏感——因为改变那个数字总是产生合数——但是97满足数位敏感的全部标准吗？答案是否定的，因为如果把十位数字改成1，得到17，一个质数。

(注意37、47和67也都是质数。)

事实上，没有两位数的数位敏感质数。下表列出了所有两位数的数字，其中质数被标记出来。

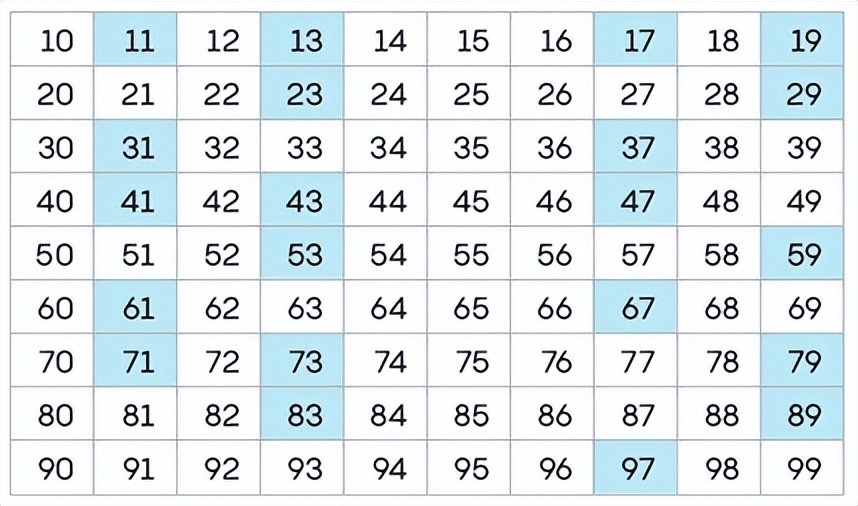
同一行

中的所有数都有相同的十位，

同一列

中的所有数都有相同的个位。97是它所处的这一行中唯一一个带阴影的数字，这说明它在个位上很敏感，但它不是这一列的唯一质数，这意味着它在十位上不敏感。

数位敏感的两位数质数必须是其行和列中唯一的质数。如表所示，不存在这样的两位数质数。那么一个数位敏感的

三位数质数

呢？下面是一个类似的表格，显示了100到199之间的三位数质数的布局，其中的合数被省略了。

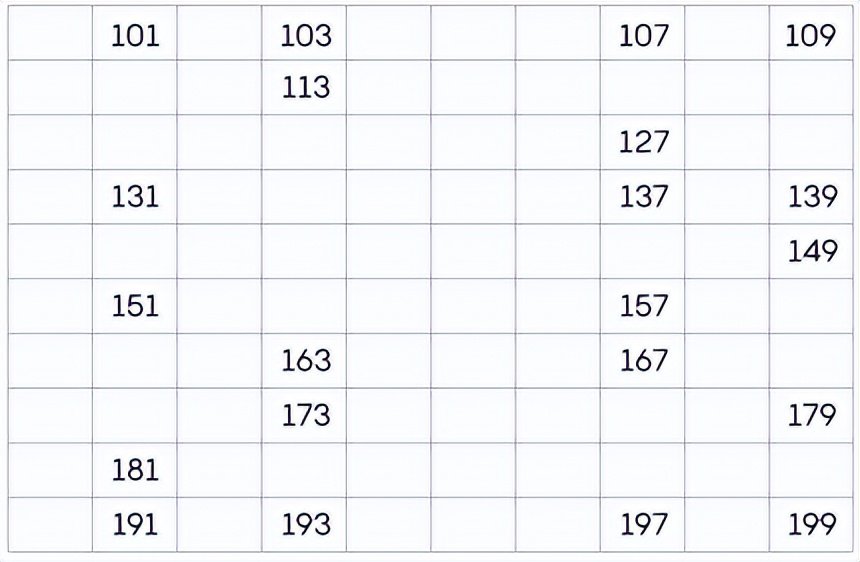
这里我们看到113独自占据一行，这意味着它在个位数上很敏感。但是113并不在它自己独占的一列中，所以对十位数字进行一些修改(比如将十位改为0得到103或改为6得到163)就产生了质数。由于没有一个数字独自在一行以及一列中，因此我们很快就会发现：如果你改变某个三位数的个位或十位数字，没有谁一定是合数。这意味着不可能有三位数的数位敏感质数。注意，我们甚至没有检查百位。要真正做到数位敏感，一个三位数的数字必须在三维表格中避开

三个方向

的质数。

数字世界中真的存在数位敏感质数吗？在数轴上越往远处质数就越稀疏，这使得它们不太可能在高维表的行和列中交叉。但更大的数字有更多的数位，每增加一个数位，成为数位敏感质数的可能性就会降低。

如果继续研究，你会发现数位敏感质数

确实存在

。最小的是294，001。当你改变其中一位数时，你得到的数字——比如794，001或284，001——将是合数。还有更多：接下来的几个是505447；584141；604171；971767；1062599。事实上，这是一个无穷数列。著名数学家保罗·埃尔德什

（Paul Erd?s）

证明了数字上有

无穷多个

数位敏感质数。这只是关于这些奇怪数字的许多令人惊讶的结果中的第一个。

例如，埃尔德什不仅证明了有无穷多个数位敏感质数：他还证明了在

任何基数

下都有无穷多个数位敏感质数。因此，如果你选择用二进制、三元或十六进制来表示数字，你仍然可以找到无穷多个数位敏感质数。

数位敏感质数并不仅仅是无限的：它们在所有质数中所占的

比例不为零

。这意味着，如果你观察数位敏感质数的数量与所有质数数量的比率，这个分数是一个大于零的数字。用专业术语来说，所有质数的“

正值的比例

”在数位上是敏感的，正如菲尔兹奖得主陶哲轩

(Terence Tao)

在2010年证明的那样。质数本身在所有数中所占的比例并不为正，因为数轴越往外，质数就越少。然而，在这些质数中，你会继续足够频繁地发现数位敏感质数，使得数位敏感质数与总质数的数量比例保持在零以上。

也许最令人震惊的发现是2020年关于这些奇怪数字的新变化的结果。通过放宽数位的概念，数学家们重新设想了数字的表示方式：他们不再只考虑97，而是认为

97前面有0

：…

0000000097。

每个前导零都可以被认为是

一个数位

，数位敏感的问题可以扩展到这些新的表示。是否存在“

广义数位敏感质数

”——如果你改变任何一个数位，包括前导的任何一个零，质数总是成为合数？由于数学家Michael Filaseta和Jeremiah Southwick的工作，我们惊奇地知道答案是肯定的。不仅存在

广义数位敏感质数

，而且它们的数量也是无穷无尽的。

质数构成了一串无穷无尽的数学谜题，供专业人士和爱好者们玩味。我们可能永远无法解开它们所有的秘密，但你可以指望数学家不断地发现和发明新的质数种类来探索。

练习

2和101之间最大的质数间隙是多少？

【答案】最大的间隙在质数89和97之间。一般来说，当你沿着数轴往外走的时候，间隙会变大，当然孪生质数猜想认为无论你往外走多远，总有离得很近的质数。还请注意，在本专栏中使用的构造质数间隙的方法是多么低效：要构造如此大小的质数间隙，你将从数字8!+2=40322开始。

【答案】并不是。考虑前六个质数：2、3、5、7、11和13。在这种情况下，数字q将是2×3×5×7×11×13+1= 30031。它不能被2、3、5、7、11或13整除，但它不是质数：它可以分解成30031 =59×509。注意它有质数因子，但它们都比前6个质数大。

【答案】如果k或q是质数，我们就证明完了。如果q不是质数，它是合数，也就是说它能被某个质数整除，但我们已经知道它不能被前n个质数整除。因此它必须能被一个大于前n个质数的质数整除；因为这些都是小于k的质数，所以这个质数一定大于k，但这个质数能除q，所以它一定小于q，所以k和q之间一定有一个质数。

4. 你能找到最小的在个位和十位数上敏感的质数吗？这意味着改变个位或十位数字总是会产生合数。(你可能需要编写一个计算机程序来做到这一点!)

【答案】第一个满足这个性质的质数是2459，因为2451、2453和2457都是合数(满足个位数敏感标准)，2409、2419、2429、2439、2449、2469、2479、2489和2499都是合数(满足十位数字敏感标准)。然而，2459并不是数位敏感质数，因为2659是质数，所以一旦你开始考虑百位数字，它就失效了。

挑战问题：用二进制表示时，你能找到最小的数位敏感质数吗？回想一下，在二进制或以2为基数的情况下，唯一的数字是0和1，每个位值代表2的幂。例如，8表示为10002，因为8=1×23+0×22+0×21+0×20，而7以2为基数表示为1112，因为7=1×22+1×21+1×20。

【答案】127=11111112是数位敏感的，因为126=11111102， 125=11111012， 123=11110112， 119=11101112， 111=11011112， 95=10111112，63=01111112都是合数。

本文经授权转载自微信公众号“中科院物理所”，编辑：藏痴。

原文链接：How Can Infinitely Many Primes Be Infinitely Far Apart?

特 别 提 示

1. 进入『返朴』微信公众号底部菜单“精品专栏“，可查阅不同主题系列科普文章。

2. 『返朴』提供按月检索文章功能。关注公众号，回复四位数组成的年份+月份，如“1903”，可获取2019年3月的文章索引，以此类推。