滴水观音养护与注意事项
2024-01-17 04:56:01
点到直线距离公式的推导过程(记住平面坐标系中点到直线距离公式的证明思想)
平面直角坐标系中直线的一般式方程为
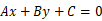
我们来推导直线外任意一点(x0,y0)到直线的距离的公式。
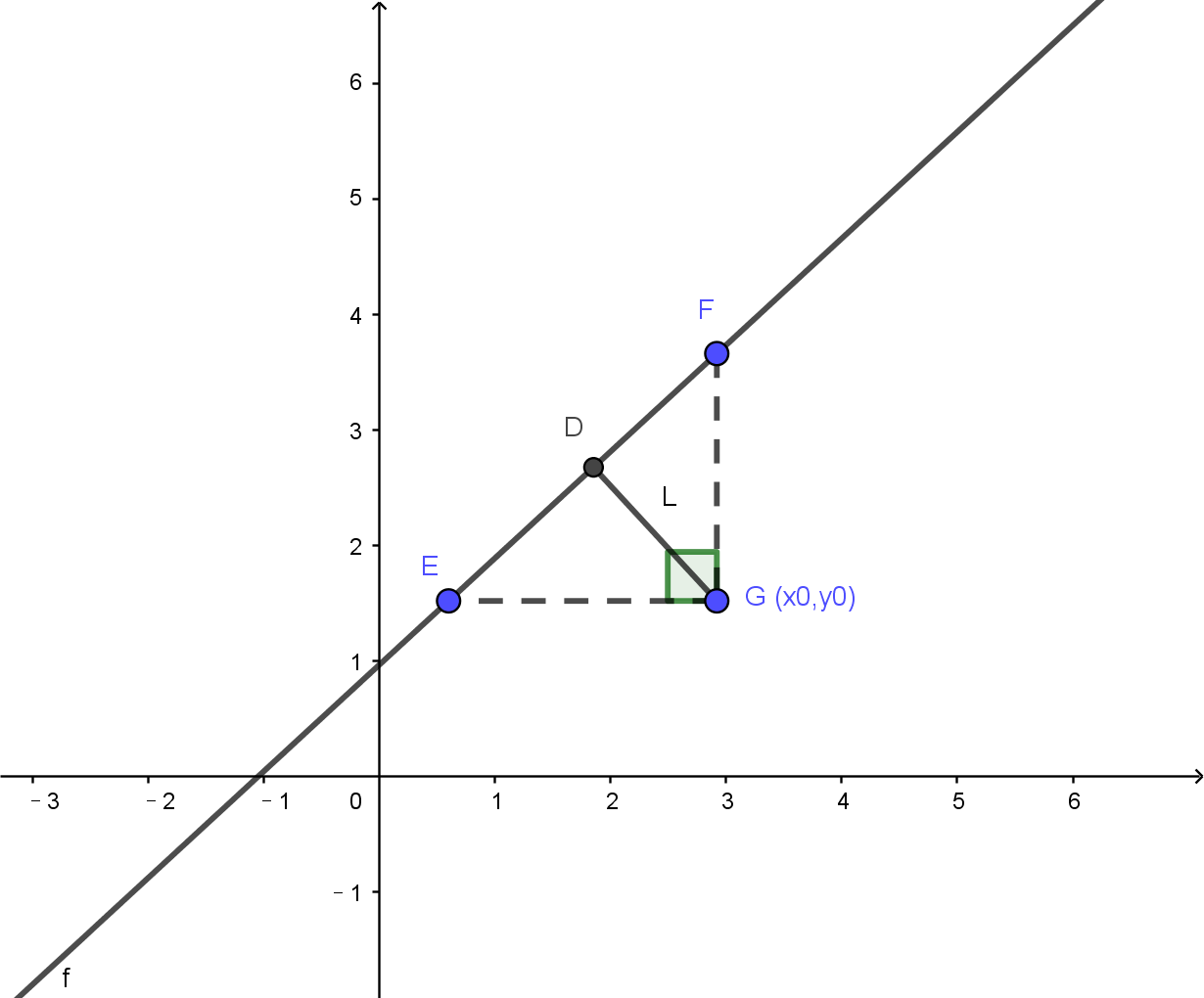
假设A、B均不为0,图中从点G(x0,y0),沿着x轴和y轴方向做两条辅助线分别交直线于E、F点,那么E的纵坐标为y0、F的横坐标为x0,将其分别带入直线的一般式方程中,
得E的横坐标为
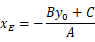
得F的纵坐标为
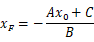
那么
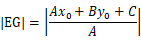
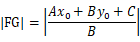
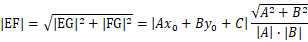
从点G向直线做垂线DG,根据三角形面积公式得
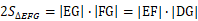
那么
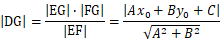
当A或B等于0时,经容易验证上述公式仍然成立。此即为直线外任意一点到直线的通用距离公式。
还有一种证明方法,证明思想是求出垂线所在的直线方程,进而求出交点D的坐标,利用两点之间的坐标公式即可求出点到直线的距离。
记住证明思想远比记住结论更重要。
2024-01-17 04:56:01
2024-01-17 04:53:56
2024-01-16 20:49:40
2024-01-16 20:47:35
2024-01-16 20:45:30
2024-01-16 20:43:25
2024-01-16 20:41:20
2024-01-16 20:39:16
2024-01-16 20:37:11
2024-01-16 20:35:06
2024-01-16 20:33:01
2024-01-16 20:30:56
2024-01-16 17:52:19
2024-01-16 17:50:14
2024-01-16 17:48:09
2024-01-16 17:46:04
2024-01-16 17:43:59
2024-01-16 17:41:54
2024-01-16 17:39:49
2024-01-16 17:37:44