​奇函数的性质f0=0,为什么奇函数f(0)=0

奇函数的性质f0=0,为什么奇函数f(0)=0

本文目录

1.为什么奇函数f(0)=0 2.所有的奇函数都有f0等于零吗 3.为什么当函数为奇函数时f(0)=0 4.奇函数为什么f(0)=0

为什么奇函数f(0)=0

因为 f(-x)=-f(x)，将x=0代入，得f(0)=-f(0)，从而f(0)=0。

奇函数特点介绍：

1、奇函数图象关于原点（0，0）对称。

2、奇函数的定义域必须关于原点（0，0）对称，否则不能成为奇函数。

3、若f（x）为奇函数，且在x=0处有意义，则

.

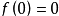
4、设f（x）在定义域I上可导，若f（x）在I上为奇函数，则f'(x)在 I上为偶函数。

即f（-x）= – f（x）对其求导f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)

扩展资料：

奇函数的性质：

1、两个奇函数相加所得的和或相减所得的差为奇函数 。

2、一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。

3、两个奇函数相乘所得的积或相除所得的商为偶函数。

4、一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。

5、当且仅当 （定义域关于原点对称）时， 既是奇函数又是偶函数。奇函数在对称区间上的积分为零。

所有的奇函数都有f0等于零吗

不一定。

因为 f(-x)=-f(x)，将x=0代入，得f(0)=-f(0)，从而f(0)=0。

奇函数特点介绍：

1、奇函数图象关于原点（0，0）对称。

2、奇函数的定义域必须关于原点（0，0）对称，否则不能成为奇函数。

3、若f（x）为奇函数，且在x=0处有意义。

4、设f（x）在定义域I上可导，若f（x）在I上为奇函数，则f'(x)在 I上为偶函数。

即f（-x）= – f（x）对其求导f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)。

奇函数的性质：

1、两个奇函数相加所得的和或相减所得的差为奇函数 。

2、一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。

3、两个奇函数相乘所得的积或相除所得的商为偶函数。

4、一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。

5、当且仅当 （定义域关于原点对称）时， 既是奇函数又是偶函数。奇函数在对称区间上的积分为零。

为什么当函数为奇函数时f(0)=0

这个不是

没有这个定义

必须有个前提是x=0时有定义时才是F(0)=0

比如F(x)=1/x

它是奇函数

但是在x=0时无定义

所以F(0)不存在

只要x=0有定义且函数为奇函数的话才有F(0)=0

奇函数为什么f(0)=0

因为 f(-x)=-f(x)，将x=0代入，得f(0)=-f(0)，从而f(0)=0。

奇函数特点介绍：

1、奇函数图象关于原点（0，0）对称。

2、奇函数的定义域必须关于原点（0，0）对称，否则不能成为奇函数。

3、若f（x）为奇函数，且在x=0处有意义，则

.

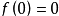
4、设f（x）在定义域I上可导，若f（x）在I上为奇函数，则f'(x)在 I上为偶函数。

即f（-x）= – f（x）对其求导f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)

扩展资料：

奇函数的性质：

1、两个奇函数相加所得的和或相减所得的差为奇函数 。

2、一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。

3、两个奇函数相乘所得的积或相除所得的商为偶函数。

4、一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。

5、当且仅当 （定义域关于原点对称）时， 既是奇函数又是偶函数。奇函数在对称区间上的积分为零。

以上就是关于奇函数的性质f0=0,为什么奇函数f(0)=0的全部内容，以及奇函数的性质的相关内容,希望能够帮到您。